Brachistochrone problem

The Brachistochrone curve is the fastest descent from point A to point B of a body subject to a gravitational force. It comes from the Ancient Greek word \(\textit{brákhistos khrónos}\) (shortest time). The description of the problem is the following. Consider two points A and B on a plane with a gravitational field acting in the \(\hat{y}\) direction. A body is released from point A and will follow curve S from point A to point B due to the gravitational force. What curve minimises the time from A to B? See figure bellow.

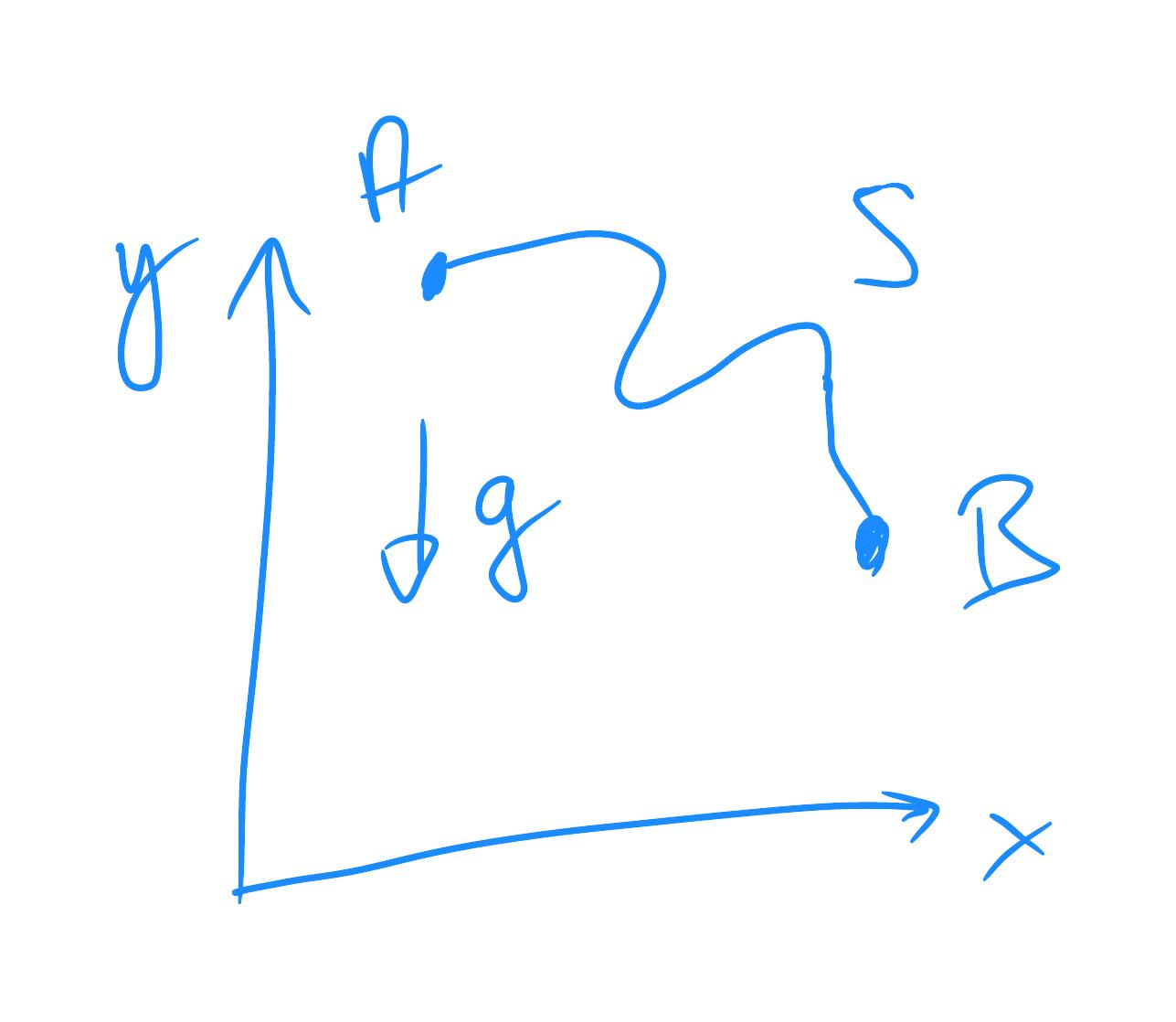
The time from A to B is given by \begin{equation} t_{AB}= \int_A ^B \frac{ds}{v}, \end{equation} where \(ds = \sqrt{dx^2+dy^2}\) is the arc length and \(v\) is velocity. A simple application of energy conservation provides us with the velocity in terms of the gravitational acceleration \(g\) and the displacement \(y\): \begin{equation} \frac{1}{2}mv^2 = mgy \Longrightarrow v = \sqrt{2gy}. \end{equation} With that, we rewrite the time expression \begin{equation} t_{AB}= \int_{x_A} ^{x_B} dx \sqrt{\frac{1+y’^2}{2gy}}, \end{equation} where we have defined \(y':= d_x y\).

We have to vary the function \(f(y,y') = \sqrt{\frac{1+y'^2}{2gy}}\) in order to solve the minimization problem. Thence, we apply the Euler-Lagrange condition \begin{equation} \partial_y f(y,y’) - d_x \partial_{y’} f(y,y’) = 0. \end{equation}

Calculating both terms: \begin{equation} \partial_y f(y,y’) = -\frac{1}{2} \sqrt{\frac{1+y’^2}{2g y^3}}, \end{equation} \begin{equation} \partial_{y’} f(y,y’) = \sqrt{\frac{1}{(1+y’^2)2g y}} y’, \end{equation} \begin{equation} d_x \partial_{y’} f(y,y’) = \sqrt{\frac{1}{(1+y’^2)2g y}} y’’ - \sqrt{\frac{1}{2g y}} y’ (1+y’^2)^{-3/2}y’y’’-\frac{1}{2} \sqrt{\frac{1}{(1+y’^2)2g }} y’^2 y^{-3/2}. \end{equation}

Inserting them into the Euler-Lagrange equation.: \begin{equation} -\frac{1}{2} \sqrt{\frac{1+y’^2}{y^3}} - \sqrt{\frac{1}{(1+y’^2) y}} y’’ + \sqrt{\frac{1}{ (1+y’^2) y}} \frac{y’^2 y’’}{ (1+y’^2)}+\frac{1}{2} \sqrt{\frac{1}{ y(1+y’^2) }} \frac{y’^2}{y} =0 \end{equation}

Multiplying the equation by \(\sqrt{y(1+y'^2)}\): \begin{equation} -\frac{1+y’^2}{2y} - y’’ + \frac{y’^2 y’’}{ 1+y’^2}+\frac{1}{2} \frac{y’^2 }{y} =0 \Longrightarrow -\frac{1}{2y} \left( 1+y’^2 \right) =\frac{y’’}{1+y’^2} -\frac{1}{2} \frac{y’^2}{y}. \end{equation} It can be simplified to \begin{equation} -2yy’’ = 1+y’^2. \end{equation} Multiplying by \(y'\), rearranging and integrating we get \begin{equation} -\int \frac{2 y’y’’}{1+y’^2} = \int \frac{y’}{y} \Longrightarrow - 2\int dx \frac{dy}{dx} \frac{d^2y}{dx^2} \frac{1}{1+y’^2} = \int \frac{dy}{dx} \frac{dx}{y} \end{equation}

As \(f(y,y')\) does not explicitly depend on \(x\), we can use the Beltrami identity \begin{equation} f(y,y’) - y’ \partial_{y’} f(y,y’) = C, \end{equation} where \(C\) is a constant. In this fashion, we have \begin{equation} \sqrt{\frac{1+y’^2}{2gy}} -\sqrt{\frac{1}{(1+y’^2)2g y}} y’^2 = C \Longrightarrow \sqrt{\frac{1}{(1+y’^2)2g y}} = C \end{equation} Squaring and rearranging we get \begin{equation} \left(1+ y’^2\right) y = k^2 \, ;\; k^2:= \frac{1}{2gC^2}. \end{equation} The equation is solved by the parametric equations of a cycloid: \begin{equation} \begin{aligned} x&= \frac{k^2}{2} \left(\theta -\sin \theta \right),
y&= \frac{k^2}{2} \left(1 -\cos \theta \right). \end{aligned} \end{equation}